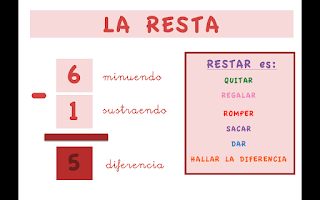
Los mismos juegos de la entrada anterior se pueden utilizar para restar, pero además podemos utilizar otros muchos más como por ejemplo:
El juego de la rayuela, en el que el alumnado deberá tirar una piedra y dependiendo de donde esta caiga tendrán que ir saltando y contando cuantos saltos dan. Luego, deberan volver a tirar la piedra y desde el lugar donde quedaron antes tendrán que ir al lugar donde ha caido la piedra. De este modo, los niños estarán realizando, inconscientemente, operaciones del tipo a+b= x.
Por ejemplo:
Si estamos en el lugar a=2 y cae la piedra en el lugar x=7, habremos dado en total b=5pasos para llegar desde el 2 hasta el 7 . De este modo, 2+b=7; b=7-2; b=5.
lunes, 28 de noviembre de 2016
¿COMO ENSEÑAR A LOS NIÑOS A SUMAR?
Algunas ideas que podemos utilizar para enseñar a nuestros menores a sumar y para trabajar la suma son:
Este es un video en el que se enseña a los padres cómo enseñar a los niños, además propone algunas actividades para repasarlas.
Este es un video en el que se muestra, cómo con un material creado con elementos reciclados, se puede enseñar a los niños a sumar. Ademas, no solo pueden aprender a sumar, sino que se puede cambiar el signo (lo podemos hacer de modo que con un velcro se quite) y podemos restar también.
 Con este material tan sencillo de hacer, podemos explicar a nuestros menores que contando dedos podemos sumar, ya que lo que habrá que hacer es contar tantos dedos como números nos digan. Este juego también es muy útil, ya que el alumnado lo relacionará con sus propias manos y las utilizará en otro momento en el que no disponga del material.
Con este material tan sencillo de hacer, podemos explicar a nuestros menores que contando dedos podemos sumar, ya que lo que habrá que hacer es contar tantos dedos como números nos digan. Este juego también es muy útil, ya que el alumnado lo relacionará con sus propias manos y las utilizará en otro momento en el que no disponga del material.
Para enseñar a mis alumnos a sumar, lo haré con juegos, ya que considero que aprender de forma ludica es la mejor manera de adquirir los conocimientos de formas mas duradera y permanente.
Por ello, un juego puede ser pintar cuadros en el suelo con números y decir a mi alumnado que de tantos pasos como números indica la suma, por ejemplo:
Dar 2 pasos y después dar 6 pasos. El niño quedará en la posición 8, y tendrá que decir que está en el lugar 8 y por tanto sumar dos mas seis son 8.
Este es un video en el que se enseña a los padres cómo enseñar a los niños, además propone algunas actividades para repasarlas.
En este video, se muestra cómo hacer un juego para que nuestro alumnado practique las sumas, e incluso se puede hacer con la resta. ademas, tambíen podemo ponerles hasta 10 y que practiquen con una mayor dificultad.
Este juego es muy util para la practica de lo aprendido previamente. Con este material tan sencillo de hacer, podemos explicar a nuestros menores que contando dedos podemos sumar, ya que lo que habrá que hacer es contar tantos dedos como números nos digan. Este juego también es muy útil, ya que el alumnado lo relacionará con sus propias manos y las utilizará en otro momento en el que no disponga del material.
Con este material tan sencillo de hacer, podemos explicar a nuestros menores que contando dedos podemos sumar, ya que lo que habrá que hacer es contar tantos dedos como números nos digan. Este juego también es muy útil, ya que el alumnado lo relacionará con sus propias manos y las utilizará en otro momento en el que no disponga del material.Para enseñar a mis alumnos a sumar, lo haré con juegos, ya que considero que aprender de forma ludica es la mejor manera de adquirir los conocimientos de formas mas duradera y permanente.
Por ello, un juego puede ser pintar cuadros en el suelo con números y decir a mi alumnado que de tantos pasos como números indica la suma, por ejemplo:
Dar 2 pasos y después dar 6 pasos. El niño quedará en la posición 8, y tendrá que decir que está en el lugar 8 y por tanto sumar dos mas seis son 8.
INICIACIÓN AL CÁLCULO: SUMA y RESTA en Educación Infantil. TEMA 5.
 Voy comenzar esta entrada diciendo
que el alumnado de educación infantil no tiene que aprender ni a sumar ni a
restar hasta los 7 años aproximadamente, pero si es necesario que los iniciemos
en estas operaciones en dicha etapa. Es decir, es conveniente que los
aproximemos a la idea de estas operaciones y facilitando su construcción
individual e interna. Primero, el alumnado de infantil, realizaran acciones
sobre los objetos, como reunir, separar, reiterar o repartir hasta que acaban
realizando sumas y restas, en torno a los 7-8 años.
Voy comenzar esta entrada diciendo
que el alumnado de educación infantil no tiene que aprender ni a sumar ni a
restar hasta los 7 años aproximadamente, pero si es necesario que los iniciemos
en estas operaciones en dicha etapa. Es decir, es conveniente que los
aproximemos a la idea de estas operaciones y facilitando su construcción
individual e interna. Primero, el alumnado de infantil, realizaran acciones
sobre los objetos, como reunir, separar, reiterar o repartir hasta que acaban
realizando sumas y restas, en torno a los 7-8 años.
Por ello, es importante que los adultos generen
situaciones de aprendizaje con material adecuado con el fin de que el alumnado
se familiarice con la resolución de problemas matemáticos.
Algunos consejos que puedo dar como estudiante
del tema son:
- Debemos
tener claro que primero, el pensamiento de los niños es intuitivo, y aprenden
por la acción,el ensayo y el error. Por tanto, deberíamos trabajar
juegos de agrupaciones, conjuntos, cantidad, etc. por ejemplo, a través de
cuentos, las rutinas de clase, etc.
- En cuanto al
material, es importante que este sea discreto y se pueda contar, agrupar y
separar, para favorecer el aprendizaje manipulativo. Además, tiene que tener un
color, tamaño, forma, grosor y textura adecuados a la edad de los/as que los
van a utilizar. Además, podemos pedir a las familias que traigan material de
casa como por ejemplo el cartón de una caja de zapatos, rollo de papel
higiénico, etc. O material estructurado como por ejemplo las
regletas o los bloques lógicos.
CARACTERISTICAS DEL
PENSAMIENTO MATEMÁTICO SEGUN LA EDAD:
La operación, desde el punto de vista
lógico-matemático, tiene dos propiedades:
- Asociativa:
puede llegarse al mismo resultado por distintos camino.
Reversible: es posible invertir la acción y
llegar al estado inicial.
Operar a los 3 años:
Lo que los niños y las niñas de infantil pueden hacer
con 3 años, es:
- Agrupar un objeto y un objeto para formar un grupo de 2.
- Separar 2 objetos que están juntos en 1 y 1. La misma actividad con 3 cosas.
- Juegos de compra y venta con precios de 1 y 2 euros y eventualmente tres.
- Iniciar el cálculo mental hasta 2 y eventualmente hasta
Operar a los 4 años:
Con esta edad, los niños son capaces de realizar
actividades de:
- Composición y descomposición de conjuntos de 3 o 4 objetos en cantidades más pequeñas, es decir en grupos de uno, o dos o tres. De muchas maneras diferentes.
- Juegos de compra y venta arribando hasta cuatro y cinco.
Operar a los 5 años:
A esta edad, los niños saben realizar actividades del
siguiente tipo:
- Dada una colección de elementos hacer prácticas de agregar y de sustraer ligadas a la primera idea de suma y resta.
- Hacer la acción de unir conjuntos ligada a la idea de sumar. Solamente a nivel manipulativo y verbal.
- Descomponer con materiales y dibujos cantidades de elementos no superiores a 7 en otras más pequeñas.
- Resolver situaciones y problemas sencillos planteados con materiales y dibujos.
- Pasar a representar en papel la situación (NO LA OPERACIÓN NUMÉRICA).
- Práctica del cálculo mental. Sobretodo que conduzca a sumar y restar.
LOS NÚMEROS PARA CALCULAR:
La
Adición es una función matemática asociada a la unión de conjuntos
disjuntos es la cardinalidad del conjunto resultante.
Los niños muchas veces memorizan el resultado de una
Adición sin un concepto real de número, desconectado en general con situaciones
de la vida real.
Podemos llegar al resultado de los problemas matemáticos
a través de la reunión o agrupación de
colecciones (la idea de reunir, agrupar o poner juntas, es espontanea del
niño) o mediante la agregación de
elementos a una colección (dando lugar al estado final)
La
Sustracción o resta es una operación inversa a la adición, ya que
implica acciones como comparar cardinales, quitar, sustraer, disminuir, etc.
EL CAMINO DE LA SUMA
Para Piaget, la suma implica
razonamiento y memoria. Por tanto considerar el todo, atribuirles a sus partes
un uso común, cualidades comunes, conservar esas impresiones, es la suma.
*Por ejemplo: bolígrafos rojos y bolígrafos azules. Estas
son todos los bolígrafos de mi estuche.
ESQUEMA DE MIALARET:
ETAPAS DE CONSECUCION DE LAS
OPERACIONES ARITMETICAS.
Las etapas por las que se construyen las operaciones aritméticas
son:
1. Partir de lo concreto
2. Representación gráfica de esa
realidad.
3. Llegar a la representación
simbólica.
En la suma y la resta, también nos podemos encontrar problemas.
è PROBLEMAS DE LA SUMA:
Añadir/transformar.
*ejemplo. Tengo
2 caramelos y mi madre me da 1. ¿Cuantos tengo?
·
Reunir/ parte-parte-todo:
*ejemplo. Hay
5 coches azules y 5 verdes ¿Cuantos coches hay?
·
Comparación:
*ejemplo. María
tiene 2 gomas y yo 3 más que ella. ¿Cuantos caramelos tengo yo?
è PROBLEMAS DE LA RESTA:
·
Quitar/ transformar:
*ejemplo. Tengo 5 caramelos y doy 2
a mi madre ¿cuantos caramelos me quedan?
·
Separar/ parte-parte-todo:
*ejemplo. Hay 3 perros y 2 son
hembras ¿cuantos machos hay?
·
Igualación:
*ejemplo. Tengo 3 caramelos y tu
tienen 5 ¿cuantos tienes tu más que yo?
·
Comparación:
*ejemplo. En un equipo de futbol hay
3 niños y 5 niños ¿cuantos más niños que niñas hay en el equipo?
Para trabajar esto con nuestro alumnado, tenemos que
pasar de menor a mayor dificultas en cuanto a los datos propuestos:
- No pasar del cinco
- Aumentar hasta 10
- Más de 10
- Aumentar hasta 10
- Más de 10
Resumido de http://matematicaseducacioninfantil.blogspot.com.es/2014/11/la-suma-y-la-resta-en-educacion-infantil.html
martes, 15 de noviembre de 2016
RESUMEN ARTÍCULO TEMA 4.
"El número natural en educación infantil: Cardinal y Ordinal"
Los niños y las niñas de infantil, necesitan aprender a contar los numeros naturales, tanto de forma ordinal como cardinal.
Debemos saber que cada elemento de un conjunto de números naturales lleva dos acepciones:
- Por el lugar que ocupa en la serie (ordinal)
- Por el significado que ese elemento tiene por sí mismo (cardinal)
*Número natural con una construcción cardinal.
Un número natural es el cardinal de un conjunto finito. Y un conjunto es infinito cuando es equipotente a una de sus partes y es finito cuando o es infinito.
*Consreucción de la secuencia numérica mediante el cardinal.
Existen diferentes pasos para secuenciar los números cardinales, como por ejemplo:
- Siguiente inmediato de un numero natural.
- Ente un número natural y su siguiente inmediato no existe ningún otro número natural.
- aeal cero no es siguiente inmediato de ningún número natural, por tanto los numeros naturales son los positivos.
*El número natural con una construcción ordinal.
La Aximática de Peano asegura que el conjunto de los números naturakes queda construido a través de diferentes axiomas.
Los axiomas de Peano establecen el cero como primer elemento.
Para todo conjunto finito A existe un único número natural, tal que hay una aplicación biyectiva entre A y el segmento inicial del conjunto de los naturales.
*Implicaciones entre el cardinal y el ordinal.
1. El postulado fundamental de la aritmetica.
2. Cálculo de distintos números cardinales mediante ordinales. Las operaciones
3. Clases de equivalencias asociadas a un número ordinal.
4. Isomorfismo de orden.
5. Número ordinal mediante cardinales.
6. Relaciones isomórficas. Entre el cardinal y el ordinal en cuanto a la construcción de la secuencia numérica.
Existen diferencias significativas entre los ordinales y cardinales.
1. Transformaciones que cambian el ordinal
2. Transformaciones que cambian el cardinal
3. Transformaciones que conservan el cardinal y el ordinal
*Epistemología genética: cardinal y ordinal
* Cardinal y ordinal: relación entre génesis.
GÉNESIS DE LA CORRESPONDENCIA CARDINAL
1. Correspondencia provocada y no duradera: poner tantos elementos de un conjunto como espacio ocupan los elementos del otro conjunto
2. Correspondencia no provocada y no duradera: actúan por correspondencia uno a uno de forma espontánea.
3. Correspondencia no provocada y duradera: exito operatorio.
Se determinan tres etapas correspondiente a la génesis de la correspondencia serial:
1. Comparación global sin seriación exacta.
2. Seriación y correspondencia progresivas e intuitivas.
3. Seriación y correspondencia inmediatas y operatorias.
*Convergencia evolutiva entre el cardinal y el ordinal.
La convergencia se establece atendiendo a que la serie numérica se aplica a una coleccion de elementos para obtener el numero cardinal. esta coleccion puede estar constituida por una serie. (Cualquier serie esta constituida por un encadenamiento de unidades).
Hay tres etapasexplicativas del desarrollo en el niño de la construcción conjunta del cardinal y ordinal:
1. Ausencia de coordinación entre el cardinal y el ordinal
2. Coordinación intuitiva entre los aspectos cardinal y ordinal del número.
3. Coordinación operatoria entre el cardinal y el ordinal.
*Orientaciones didácticas.
Suscribirse a:
Comentarios (Atom)